- Neste tópico, vamos estudar as distribuições de probabilidades, este tipo de modelo busca estimar uma população, a partir de uma amostra.
Por exemplo, suponha que você estuda os efeitos em um grupo de pessoas, visando descobrir como elas reagem a determinado medicamento. Após analisar os dados da pesquisa, é possível inferir o comportamento para toda a população, achando a probabilidade de haver determinados efeitos colaterais, tempo efetivo de tratamento, dentre outros indicadores.
É bom deixar claro que, as distribuições probabilísticas, são estimadores. Isso significa que, não necessariamente você conseguirá descrever o comportamento de determinada população, apenas aplicando esta ferramenta estatística, em uma amostra.
Neste momento, vamos estudar duas distribuições simples: a distribuição de Bernoulli e a distribuição Gaussiana (também conhecida como distribuição Normal). A primeira delas é utilizada para variáveis discreta, enquanto a última é aplicada em variáveis contínuas.
1) Distribuição de Bernoulli
Vamos aplicar, inicialmente, o que é uma variável discreta. Este tipo de variável assume valores finitos, podendo ser qualitativa ou quantitativa.
No tocante às variáveis qualitativas, podemos citar as pesquisas de satisfação, onde a resposta a pesquisa é algo como "bom", "ruim, e etc… Ou, um valor de 1 a 10.
Em relação às variáveis quantitativas, são aquelas cujos valores pertençam ao conjunto dos inteiros (Z = {…, -3, -2, -1, 0, 1, 2, 3, …}).
Após essa rápida explicação. A distribuição de Bernoulli é utilizada para avaliar a probabilidade de êxito (p), de determinado acontecimento que se repente N vezes, e tem resultado exitoso k vezes. A fórmula que descreve essa distribuição é:
p(k) = CN,k*pk*(1 – p)N – k
Vejamos um exemplo: Qual a probabilidade de cair a face seis, quatro vezes, em nove lançamentos de um dado comum?
Nesse caso, o êxito é aparece a face seis em um dado comum é p = 1/6. O número de tentativas é N=9, e o número de êxito é k=4. Assim, vamos calcular primeiro a combinação presente na fórmula (você notou?):
C9,4 = 9!/(4!*(9 – 4)!) = 9*8*7*6*5!/(5!*4*3*2*1) = 9*8*7*6/(4*3*2*1) = 126
Continuando,
p(4) = 126*(1/6)4*(1 – 1/6)9 – 4 = 126* 0,000772*0,402 = 0,00391 = 0,391%
Note que este tipo de amostra é uma excelente ferramenta para indicar risco de falhas, ou, no controle de qualidade, avaliando o número de produtos defeituosos, e determinado lote, a partir de uma amostra aleatória.
Por exemplo, suponha que sua empresa recebeu a encomenda de 10.000 unidades de determinado produto. O controle de qualidade testou 100 destas unidades, encontrando 2 defeituosas. Qual a probabilidade de 10% do lote esteja defeituoso?
Neste caso, o "êxito" é a probabilidade de uma unidade estar defeituosa. Como foram encontradas 2 em uma amostra de 100, a probabilidade é de 2/100, 0,02 ou 2%.
O total de tentativas é igual ao número de unidade total N=10.000 e a quantidade de "êxito" é 10% de N. Ou seja, 1.000 unidades.
Dessa forma, temos:
C1000,100 = 1000!/[100!*(1000-100)!] = 1000!/(100!*900!) = 6,38*10139
p(1000) = 6,38*10139*(0,02)100*(1 – 0,02)1000 – 100 = 6,38*10139*1,27*10-170* 1,27*10-
p(1000) = 10,29*10-39 = 1,029* 10-38
Veja que este valor tem 38 casas decimais! Ou seja, é pouquíssimo provável que este lote tenha 10% de peças defeituosa.
É importante deixar claro, que este resultado depende da amostra avaliada. Assim, se o controle de qualidade tivesse escolhido outras unidades, ou um tamanho diferente de amostra, o resultado poderia ser outro.
Para finalizar os estudos da distribuição de Bernoulli, vamos conhecer algumas propriedades:
→ A soma das probabilidades de todos os valores de k (0, 1, …, N) é igual a 1.
→ A probabilidade de (k < X) é igual a soma de todos os valores de k, de (X – 1) até 0-. Exemplo:
p(k < 4) = p(k=3) + p(k=2) + p(k=1) + p(k=0)
→ A probabilidade de (k > X) é igual a soma de todos os valores de k, de (X + 1) até N-. Exemplo para N = 6:
p(k > 3) = p(k=4) + p(k = 5) + p(k=6)
→ p(k > X) = 1 – p(k ≤ X). Exemplo:
p(k>3) = 1 – (p(k=3) + p(k=2) + p(k=1) + p(k=0))
- → O valor esperado para uma variável que segue a distribuição de Bernoulli é N*p, onde p é probabilidade de êxito.
→ A variância desta distribuição é N*p*(1 – p).
Existem diversas distribuições de probabilidade para variáveis contínuas. Neste projeto, ficaremos somente com a distribuição de Bernoulli.
No tocante a distribuições em variáveis contínuas, vamos estudar a distribuição Gaussiana (ou Normal).
2) Distribuição Gaussiana
Assim como antes, vamos entender o que significa uma variável contínua. Este tipo de variável é iminentemente quantitativa, podendo assumir infinitos valores. Dessa maneira, a variável contínua está no domínio dos números reais (R).
Essa distribuição assume que o valor com maior probabilidade é a média (XM), e conforme nos afastamos dela, para valores maiores ou menores, a probabilidade vai diminuindo, até, no limite, se tornar muito próximo de zero.
A função da densidade de probabilidade, ou seja, a probabilidade para cada valor (x) assumido pela variável (X) é:
p (X = x) = (1/√2*π*s²)*exp{-0,5*[(x – μ)/s²]}
Na função, s é o desvio-padrão da população, e μ é a média da população. Caso não se tenha toda a população, mas sim, uma amostragem, utilizamos a média desta amostra (XM) e seu desvio-padrão (ϭ).
Desse jeito, para inferirmos o comportamento de uma população, a partir de uma amostra, a função se destaca:
p (X = x) = (1/√2*π*ϭ²)*exp{-0,5*[(x – XM)/ϭ]²}
Vejamos agora o gráfico com alguns exemplos da distribuição normal, para alguns valores de média e desvio-padrão.
Note como a curva se comporta, em relação à média. Como dito antes, a função gera um padrão simétrico em torno da média. Veja também que, a curva com o menor desvio-padrão (verde, s=0,5) apresenta maior concentração de probabilidades muito próximo à média, o contrário ocorre na curva amarela (s=2).
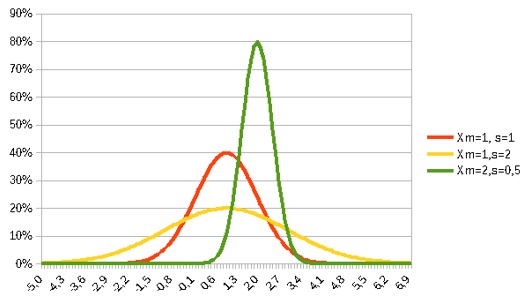
Figura 8: Funções densidade de probabilidade da distribuição Gaussiana.
Fonte: Do autor.A função de densidade calcula o valor específico de probabilidade, para cada valor. Mas, com a variável estudada é contínua, faz mais sentido avaliar um intervalo de valores. Nesse caso, precisa da função de distribuição acumulada. A determinação matemática desta função acumulada é muita complexa. Por isso, foi criada uma tabela que nos ajuda a determinar a probabilidade acumulada.Como utilizar esta tabela? Inicialmente devemos encontrar a variável Z, em que: Z = (x – XM)/ϭApós isso, é podemos começar a ler a tabela. Note que a unidades e a primeira casa decimal estão nas linhas, enquanto a segunda casa decimal está nas colunas. Ou seja, para encontrar a probabilidade de Z = 1,87, você deve ir até a linha "1.8" e a coluna ".07". Para este Z, o valor encontrado na tabela é 0,4693 (.4693). Para determinar a probabilidade, é precisa se atentar ao seguinte detalhe:→ Se Z = 1,87 (positivo), então, p(Z ≤ 1,87) = 0,5 + 0,4693 = 0,9693 (96,93%)→ Se Z = - 1,87 (negativo), então, p(Z ≤ - 1,87) = 0,5 – 0,4693 = 0,0307 (3,07%)Três constatações importantes: *Caso você encontre Z < 0, é preciso que você procure na tabela o módulo (sem sinal),*É preciso adicionar ou subtrair 0,5 ao valor encontrado, para determinar a probabilidade, e;* Essa tabela só calcula a probabilidade acumulada para valores menores ou iguais a Z.Talvez um exemplo facilite seu entendimento:Suponha que a demanda por certo produto tem uma média de 8.000 unidades/mês, com um desvio-padrão de 3.500 unidades/mês. Qual a probabilidade da demanda ser menor ou igual à 4000 unidades/mês?Para usar a tabela, devemos calcular o valor de Z: Z = (4000 – 8000) /3500 = -1,14Na tabela, procuramos o módulo de Z (1,14). O valor encontrado é 0,3729 (.3729).Como o nosso Z é negativo, subtraímos este valor de 0,5: p (Z≤-1,14) = 0,5 – 0,3729 = 12,71%Assim, a probabilidade da demanda ser menor ou igual à 4000 unidades/mês é 12,71%. Nota: Esta probabilidade é correta se a população do fenômeno estudado se comportar de forma semelhante a distribuição Normal. Vamos a mais um exemplo: A média de altura de determinada população é 170 cm, com desvio-padrão de 25 cm. Caso se construa uma casa com portas de 190 cm de altura, qual a probabilidade de uma pessoa ter que se abaixar para cruzá-las?Calculando Z = (190-170)/25 = 0,8, encontramos a entrada .2881 (0,2881) na tabela. Como o nosso Z é positivo, a probabilidade é p(Z ≤ 0,8) = 0,5+0,2881 = 0,7881 = 78,81%.Essa é a resposta? Não. As pessoas que devem se abaixar têm mais de 190 cm, e, a probabilidade encontrada é para pessoas menores ou iguais de 190 cm. Então, a probabilidade que procuramos é o quanto falta para completar os 100%: p(Z>0,8) = 1 - p(Z ≤ 0,8) = 1 – 0,7881 = 21,19%Veja o último exemplo: Medições de pressão em determina tubulação mostram valores que se ajustam a uma distribuição Gaussiana, com média 28 Kgf e desvio-padrão de 6 Kgf. Se a faixa ótima de operação ocorre entre 25 Kgf e 30 Kgf, qual a probabilidade de encontramos uma medição dentro desta faixa ótima?Nesse caso, queremos a probabilidade entre valores. Mas, a tabela não nos dá este tipo de informação de forma direta. A solução é:Calculamos um valor Z para cada extremo do intervalo (25 e 30): Z = (25 – 28)/6 = -0,5 e Z
= (30 – 28)/6 = 0,33Procuramos os valores da tabela para os dois valores de Z. Para Z = 0,5, o valor será 0,1915, enquanto para 0,33, 0,1293.Agora, vamos as probabilidades: p(Z≤-0,5) = 0,5 – 0,1915 = 0,3085 = 30,85% p(Z≤0,33) = 0,5 + 0,1293 = 0,6293 = 62,93%Em nosso problema, procuramos p(-0,5 ≤ Z ≤ 0,33). Para resolver a probabilidade deste intervalo: p(-0,5 ≤ Z ≤ 0,33) = p(Z≤0,33) – p(Z≤-0,5) = 62,93% - 30,85% = 32,08%Indicações de leituraPara afixar os conhecimentos, leia os capítulos 2 e 3 (especificamente, os itens 3.1.1 e 3.2.3), do livro "Introdução à Estatística".
Vamos praticar a teoria? Veja na sequência um vídeo com exercícios, sobre os conteúdos abordados nesse tópico.
No vídeo a seguir, veremos na prática o que acabamos de estudar:
- → O valor esperado para uma variável que segue a distribuição de Bernoulli é N*p, onde p é probabilidade de êxito.