Em matemática, a identidade de Euler é representada pela equação
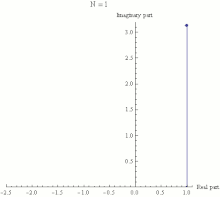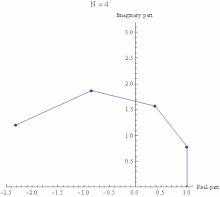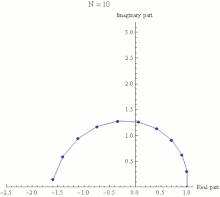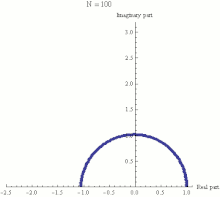
A
função exponencial natural ez pode ser definida como o
limite de
(1 + zN)N, quando
N tende ao infinito, e assim
eiπ é o limite de
(1 + iπN)N. Nesta animação
N assume vários valores crescentes de 1 a 100. O cálculo de
(1 + iπN)N é mostrado como efeito combinado de
N multiplicações repetidas no
plano complexo, com o ponto final sendo o valor de
(1 + iπN)N. Pode ser visto que quando
N cresce
(1 + iπN)N aproxima o limite −1.
- {\displaystyle e^{i\pi }+1=0}
.
Segundo Richard Feynman seria a identidade mais bela de toda a matemática. A equação aparece na obra de Leonhard Euler Introdução, publicada em Lausanne em 1748. Nesta equação, e é a base do logaritmo natural, {\displaystyle i}
é a unidade imaginária (número imaginário com a propriedade i² = -1), e {\displaystyle \pi }
é a constante de Arquimedes pi (π, a razão entre o perímetro e o diâmetro de qualquer circunferência).
A beleza da equação é que ela relaciona cinco números fundamentais da matemática: e, pi, i, 0 e 1; e as operações base da matemática: adição, multiplicação e exponenciação.
Demonstração da Identidade de EulerA série de Taylor, de forma geral, é enunciada como,
{\displaystyle f(x)=\sum _{n=0}^{\infty }{f^{(n)}(a)(x-a)^{n} \over n!}}
.
Quando aplicamos a série para a função exponencial, nós encontramos que,
{\displaystyle e^{x}=e^{a}(x-a)^{0}+e^{a}{(x-a)^{1} \over 1!}+e^{a}{(x-a)^{2} \over 2!}+...}
para a série centrada no ponto {\displaystyle a=0}
,
{\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}}
.
Esta função exponencial complexa tem as mesmas propriedades que a função exponencial real. Disso concluímos que {\displaystyle e^{z_{1}+z_{2}}=e^{z_{1}}.e^{z_{2}}}
e se fizermos {\displaystyle z=iy}
onde {\displaystyle y}
é um número real, obteremos:{\displaystyle e^{iy}=1+iy+\left({\frac {(iy)^{2}}{2!}}\right)+\left({\frac {(iy)^{3}}{3!}}\right)+\left({\frac {(iy)^{4}}{4!}}\right)+\left({\frac {(iy)^{5}}{5!}}\right)\cdots =1+iy-\left({\frac {y^{2}}{2!}}\right)-i\left({\frac {y^{3}}{3!}}\right)+\left({\frac {y^{4}}{4!}}\right)+i\left({\frac {y^{5}}{5!}}\right)\cdots }
{\displaystyle =1-\left({\frac {y^{2}}{2!}}\right)+\left({\frac {y^{4}}{4!}}\right)-\left({\frac {y^{6}}{6!}}\right)\cdots +i[y-\left({\frac {y^{3}}{3!}}\right)+\left({\frac {y^{5}}{5!}}\right)\cdots ]}![{\displaystyle =1-\left({\frac {y^{2}}{2!}}\right)+\left({\frac {y^{4}}{4!}}\right)-\left({\frac {y^{6}}{6!}}\right)\cdots +i[y-\left({\frac {y^{3}}{3!}}\right)+\left({\frac {y^{5}}{5!}}\right)\cdots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79bfb0370b58321d60e9624717f62105a4f9cef7)
{\displaystyle =\sum _{n=0}^{\infty }{(-1)^{n}y^{2n} \over (2n)!}+i\sum _{n=0}^{\infty }{(-1)^{n}y^{2n+1} \over (2n+1)!}}
,
as duas séries são as famosas séries das funções {\displaystyle cos(y)}
e {\displaystyle sen(y)}
, respectivamente. Portanto, vemos que a função exponencial com argumento complexo será
{\displaystyle e^{iy}=cos(y)+i\,sen(y)}
.
aplicando para {\displaystyle y=\pi }
{\displaystyle e^{i\pi }=-1\,\,\,\rightarrow \,\,\,e^{i\pi }+1=0}
 | Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o.
ref.: https://pt.m.wikipedia.org/wiki/Identidade_de_Euler
Cálculos: https://www.mathway.com/pt/Calculus |
