[...] Sendo c um número real, considere a função afim f (x) = 2x + c, definida para todo número real x.

Sendo c um número real, considere a função afim f (x) = 2x + c, definida para todo número real x.

a) Encontre todas as soluções da equação [f (x)]3 = f (x3), para c = 1.

b) Determine todos os valores de c para os quais a função g (x) = log(xf(x) + c) esteja definida para todo número real x. 

Resolução

Portanto, as soluções são 0 e –1.

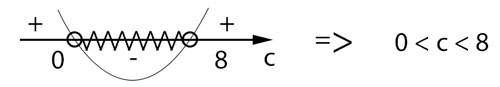
Portanto, 0 < c < 8.